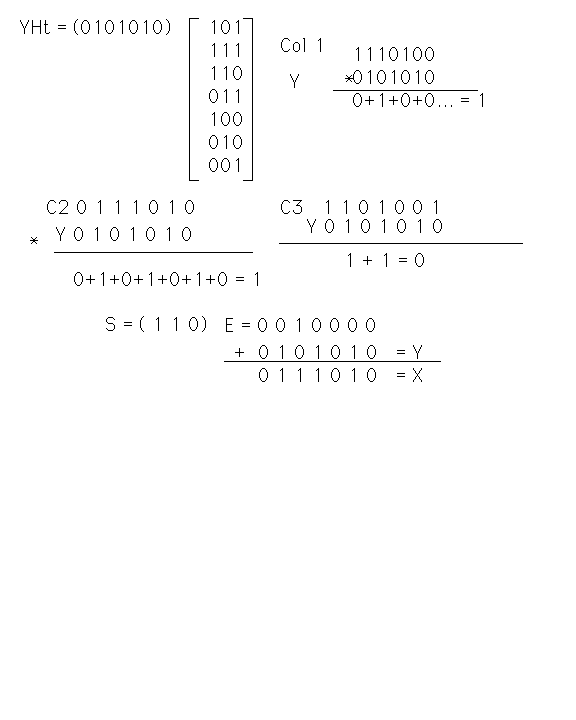Hamming codes are (n,m) linear block codes with the number of check bits equal to:
![]()
![]()
![]()
Single error correction or double error detection.
Let
![]()
To formulate the P submatrix, use Hammings rule:
Let the m rows of P have all k(=3) bit words with 2 or more 1's in any order.
A generator matrix, G, is defined such that when multiplied by the message vector, M, the code word X results.
![]()
where
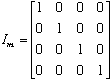
=[4x4] identity matrix (for a (7,4) hamming code)
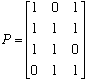
=[4x3] thus:
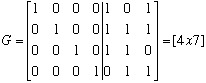
G = nxm generator matrix for the
(n,m) hamming
code.
Let M = a block
of m message
bits (4 bits for a (7,4) code).
Let C= a block
of k check bits
(k=3 bits = 7-4,
for a (7,4) code)
Let X = code vector of n bits, such that:
![]()
A code vector is obtained by the formula:
![]()
The check vector is obtained via:
![]()
Let W(x) be the scalar weight of a code word, so, for the first 8 of the 16 code words, we can compute a table:

Let X= transmitted code word and Y= code word received.
if
![]()
a transmission error was made, but the converse is
not always true.
Let
![]()
So that
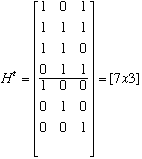
Please verify, for yourself, that
![]()
provided that
X is a code vector.
Let E be an
error vector which shows where a single bit error has occured in an
n bit code
word.

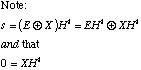
So s depends only on the error vector, E and is computed, simply, as:
 ,S
,S![]()
At the rcvr, we compute
![]()
and find out where the error happened.