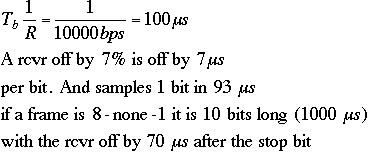
4. Digital Data Communication Techniques
Asynchronous xmission := trasmission in which each character of the information is synchronized individually (usually by the use of start and stop elements). For example, in EIA-232 there is always 1 start bit and 1-2 stop bits.
Sometimes error detection or correction codes are included as part of the xmission standard. In EIA-232 a parity bit is sometimes used. Odd parity makes the data+parity odd, Even parity makes it even. 8-none-1 = 8 data bits, no parity and one stop bit (lowest overhead EIA-232 xmission)
The stop bit is the same as the idle state, so there is no max number of stop bits.
frame :=A character + framing bits
framing bits := sync bits := noninformation-carrying bits used to make possible the separation of characters in a bit stream.
framing error := incorrect grouping of the frames
Framing error occurs if the rcvr misses a bit by sampling at the wrong rate.
For example: R= data rate = 10000 bps
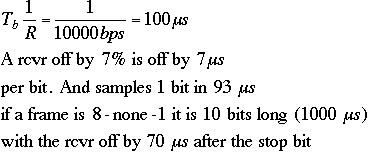
Synchronous xmission
Synchronous xmission := xmission where the rcvr and xmitter operate at the same frequency and are held in a desired phase relationship by correction devices.
The clocks are often xmitted on a channel (wire) which is the same as the data. For example, in self-clocking codes, (i.e. FM-0, a biphase space code used in localtalk) each bit cell contains a transistion at each end that provides timing information know as one bit-time. Zeros are encoded by adding a transition at midcell.
An alternative is to xmit the clock on a different channel than the data (extra wire).
Frames are still needed in synchronous xmission, but they may be longer and therefore have less overhead. The control bits are called the preamble and postamble. Sometimes the postamble is not needed because the frame length is contained in the preamble.
Character oriented data uses chars to group the bits for data and control. Bit-oriented data does no such grouping. Bit-oriented xmission refers to the preamble as a flag.
How to construct the frame is a data link layer issue. The use of async vs sync xmission is a physical layer issue. For example: tolkentalk, ethertalk and localtalk are data link access protocols.
The token ring, ethernet and localtalk hardware are in the physical layer. It is often the case that people confuse LocalTalk Link Access Protocol with the LocalTalk hardware, they are different things.
While LocalTalk Link Access Protocol is always used with Local Talk hardware, the protocol choice is not always an indication of which hardware will be used.
Example: IP := Internet Protocol. The protocol that provides the packet delivery service on the ARPANET. There exist implementations of IP (SLIP) which run on RS-232 (from 1200 bps to 19.2 kbps), token rings, satellite links and packet radio.
Error Detection Techniques (read Chapter 4 in Tannenbaum).
No matter how the physical layer is designed, there is a non-zero probability that an error will occur during xmission.
 A Class 1 error
occurs with prob.
A Class 1 error
occurs with prob. ![]() ...
...
Suppose there is no error detection scheme, then ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Example: at 300 bps (Bell 103) on a phone line, ![]()
![]()
![]()
![]()
one frame every 1000 will be in error. Since every frame is a character, then 1 char in 1000 chars will be in error.
Error detection bits are added to a frame and increase overhead, but decrease the chance of an undetected error.
Parity Checks
When a single bit is used as parity the the probability of a class 2 (undetected) error occuring is obtained via the binomial distribution.
Summary of Binomial Distributions
The binomial model describes an integer-valued discrete r.v.
asociated with repeated trials of an experiment. Repeat an experiment
n times and count the number of times a certian event A
occurs, and you have implicitly defined the binomial random
variable I whose possible values are the integers, ![]() . This model applies to repeated
coin tossings when I stands for the number of heads in
n tosses. It also applies when I stands for the number
of errors in a message of n digits.
. This model applies to repeated
coin tossings when I stands for the number of heads in
n tosses. It also applies when I stands for the number
of errors in a message of n digits.
Let the event A under consideration have ![]() . Any sequency of n
independent bits in which A occurs i times then has the
probability
. Any sequency of n
independent bits in which A occurs i times then has the
probability ![]() . The number of
such sequences is given by the binomial coefficient, denoted
as
. The number of
such sequences is given by the binomial coefficient, denoted
as ![]() . Therefore,
the binomial frequency function is
. Therefore,
the binomial frequency function is ![]()
![]()
it is understood that 0!=1 when i=n or i=0
N! is often hard to compute on a computer..esp if you only have 2 digits of exponent...for example 70! cannot be computed on some calculators since it is greater than 10**99.
Stirling's Approximation [Roberts 1984]
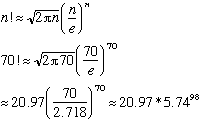
Using Maple, we can compute N! to any number...
plot(log(n!),n=0..500);
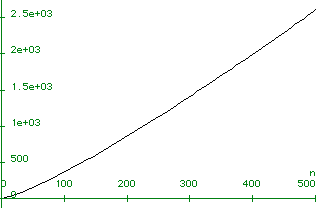
plot(log(n!),n=0..50000);
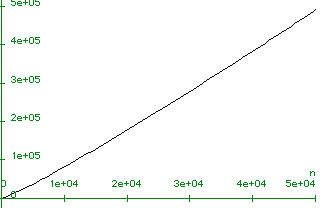
How does maple do this? Maple computes the integer factorial exactly. Recall that the set of integers is closed under multiplication, so:
* 50!;
30414093201713378043612608166064768844377641568960512000000000000
_
* 500!;
122013682599111006870123878542304692625357434280319284219241358838584537315\par 388199760549644750220328186301361647714820358416337872207817720048078520515\par 932928547790757193933060377296085908627042917454788242491272634430567017327\par 076946106280231045264421887878946575477714986349436778103764427403382736539\par 747138647787849543848959553753799042324106127132698432774571554630997720278\par 101456108118837370953101635632443298702956389662891165897476957208792692887\par 128178007026517450776841071962439039432253642260523494585012991857150124870\par 696156814162535905669342381300885624924689156412677565448188650659384795177\par 536089400574523894033579847636394490531306232374906644504882466507594673586\par 207463792518420045936969298102226397195259719094521782333175693458150855233\par 282076282002340262690789834245171200620771464097945611612762914595123722991\par 334016955236385094288559201872743379517301458635757082835578015873543276888\par 868012039988238470215146760544540766353598417443048012893831389688163948746\par 965881750450692636533817505547812864000000000000000000000000000000000000000\par 000000000000000000000000000000000000000000000000000000000000000000000000000\par 0000000000
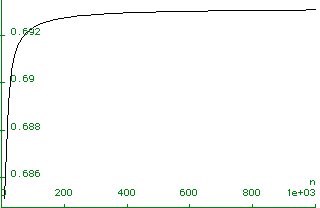
* plot({log(2*sqrt(2*Pi*n)*(n/E)**n)-log(n!)} ,n=0..1000);
This is not just a function of the number of digits to which an approximation is performed:
*evalf(log(2*sqrt(2*Pi*10000)*(10000/E)**10000)-log(10000!));
.69314
*Digits:=30;
evalf(log(2*sqrt(2*Pi*100)*(100/E)**100)-log(100!));
.692313850004310394733850880
The CDF (cumulative distribution function) is
![]()
![]()
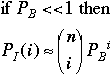
Which is the prob. of i errors in an n bit codeword.
Properties of Binomial Coefficients
![]()
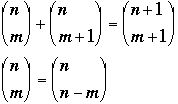
since 0!=0,
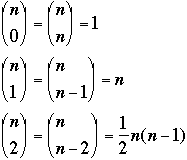
recall

![]()
![]()
![]()
![]()
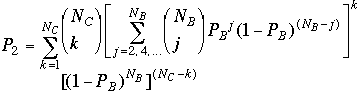
![]()
Note: the parity bit reduces ![]()
The problem is that noise is sometimes bursty and affects more than one bit in a sequence. For this reason, we may introduce more than one parity bit. Suppose we introduce row parity.
row parity := the parity but at the end of each character
longitudinal redundancy check (LRC) := checksum
checksum:=a logical sum of data that is included in a record as a guard against recording of transmission errors
longitudinal parity :=LRC

![]()
![]()
![]()
![]()
This reduces class 2 error prob. by 100 to 10000 times.
To do even better we can use the CRC...
Cyclic redundancy check (CRC):=an error-detecting code generated from a polynomial that can be added to a data record or sector.
![]() excluding the
FCS.
excluding the
FCS.
Frame check sequence (FCS) := an n-bit sequence which, when added to a k-bit frame, makes the k+n bits exactly divisible by a predetermined number.
mod-2 addition (and subtraction) uses x-or with no carries: Ex:
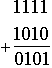
binary multiplication works as follows:
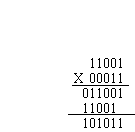 note the x-or
addition here.
note the x-or
addition here.
Let
![]()
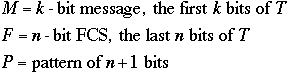
P is the predetermined divisor.
Want T/P to have no remainder so:
![]()
Where ![]() performs a
left shift by n bits and pads out the results with 0's.
performs a
left shift by n bits and pads out the results with 0's.
![]() where Q is the
Quotient and R/P is the reminder (Frame check sequence, FCS).
where Q is the
Quotient and R/P is the reminder (Frame check sequence, FCS).
CRCs are used by several protocol's:
xmodem, x.25, CRC-CCITT, kermit, HDLC (ISO), SDLC (IBM bisynch), ISBN
(International Standard Book Number), MasterCard accounts, bar zip
codes, Token Ring and Ethernet.
CCITT= Comité Consultatif International Télégraphique et Téléphonique
If the underlying data-link and network layers are unreliable, the transport layer must provide an end-to-end check. This is how TCP and UDP operate. You may disable UDP checksum's, however.
The global variable, udpcksum, in the kernal may be examined with a debugger (given proper permission). If it is 0, UDP checksums are not computed for outgoing UDP packets.
Ethernet uses a 32 bit CRC appended to every ethernet Frame.
A generatory polynomial, G, of degree M may be written as either a polynomial or as a bit-string, e.g., 10001000000100001 for CCITT.
Math is that of polynomials over integers modulo 2. Binary message = polynomial with coefficients 0 and 1. For example
![]()
Since 0 and 1 are only integers mod 2, a power of x is either present or absent.
An M-bit CRC is based on a particular primitive polynomial of degree M.
Primitive polynomial = unique factorization
For example:
![]()
is not a primitive polynomial (recall mod two arithmetic) but
![]()
is a primitive polynomial.
See numerical recipes in (C, Pascal or FORTRAN) for a software implementation..
Example on pp210 TannenbaumAnother way to view the CRC:
Express polynomials in a dummy variable, X, with binary coeffs. Ex: M=message=110011 so:
![]()
For P=Pattern=11001: ![]()
Arithmetic operations are mod 2. CRC is described as:
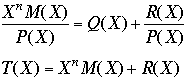
G(x)=generator polynomial
m=# of message bits
r= degree of G(x)
given the frame 1101011011 and ![]() find the check sum which must be appended to the frame
so that the frame, when divided by the G(x) has no remainder.
find the check sum which must be appended to the frame
so that the frame, when divided by the G(x) has no remainder.
The generator has 10011 as the binary representation of the generator polynomial of degree 4.
![]()
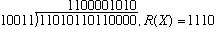 ,T(x)=M(x)+R(x)
,T(x)=M(x)+R(x)
G(x) = 10011
and M(x) = 1101011011
With the number of check bits equal to k=4, we compute the remainder, R(x) as follows:
_____1100001010
10011) 11010110110000
10011
-----
010011
10011
-----
010110
10011
-----
10100
10011
-----
1110 = R(x)
so that
T(x)= 11010110111110
Now the receiver will take T(x) and divide it by the generator polynomial, G(x). If the remainder is zero then no error was detected.
_____1100001010
10011) 11010110111110
10011
-----
010011
10011
-----
010111
10011
-----
10011
10011
-----
00 = R(x)
so no error was detected!