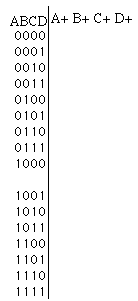

Please write your Student ID#:____________________________
Instructions/Please Read Carefully!
In taking this examination, you agree that all work recorded herein is your own. A student caught in the act of cheating will be given a grade of F on this examination and a letter will be written to his or her file.
Read the questions carefully. If something appears ambiguous, raise your hand and ask, the exam may have bugs.
Points have been assigned according to the formula such that 2 points = 1 exam minute, so pace yourself accordingly. There are 100 points on this test and you have 50 minutes to complete the exam.
Please be sure to answer all questions. A partly answered question may be awarded some points. An blank question is awarded no points.
Please check over your work, if you have extra time. Points are not awarded for tests handed in early.
All work is to be done on the attached sheets and under no circumstances are blue books or loose sheets to be used. Write your name at the top and do not proceed until your are told to do so.
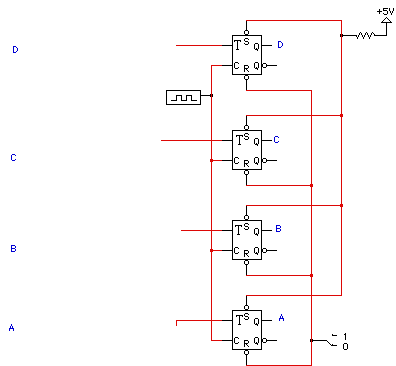
1. A 4-bit Johnson counter advances through the sequence D C B A = 0000,1010,0110,0011,1101,0001,1111,1000, and repeats. Show how to implement the Johnson counter using T flip-flops. Fill-in the Remapped FF inputs and K-maps, and show a schematic for the minimized sum of pruducts implementation of the Next State function in the box next to the flip-flops. You may assume that an external reset signal places the counter in state 0000 when asserted. DO NOT make the counter self-starting.
a) Draw the state-transition diagram next to the remapped FF table below. (10 points)
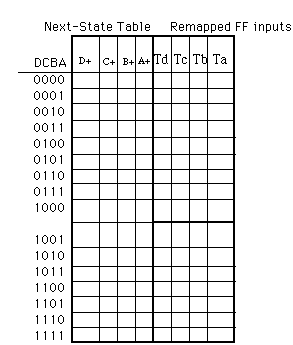
b) Write the next-state table (10 points) and the remapped FF inputs (10 points).

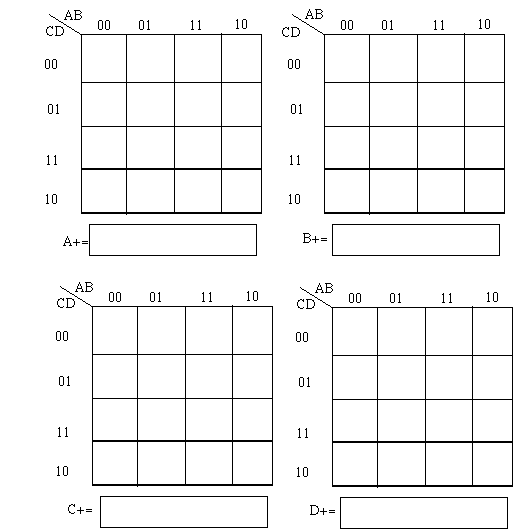
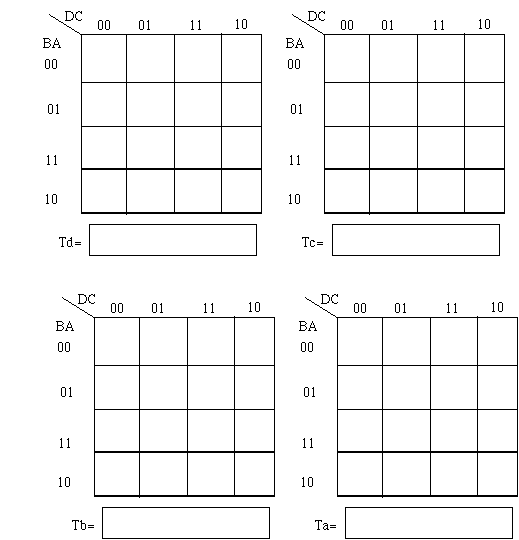
c) in the k-maps below, number the k-maps and fill them out with the remapped FF-inputs. (10 points)
d) Loop the k-maps and write the minimum sum-of-products form in the space provided. (10 points)
e) Draw the circuit using AND gates and OR gates which implements the logic shown in your k-maps. (10 points)
2. The basic functionality of a J-K flip-flop can be implemented by a D flip-flop. Show that this is true by comparing the characteristic equations. (10 points)
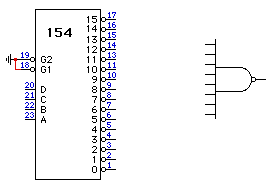
3. (20 points) A decoder together with an NAND gate connected to its output terminals, can be used in the synthesis of combinational networks. Using one 4:16 decoder (74154) and an 8-input NAND gate (7430), implement the function F(A,B,C,D)=A'B'D+A'BD+AC'D+ACD'
A B C D F 0 0 0 0/ 0 0 0 1/ 0 0 1 0/ 0 0 1 1/ 0 1 0 0/ 0 1 0 1/ 0 1 1 0/ 0 1 1 1/ 1 0 0 0/ 1 0 0 1/ 1 0 1 0/ 1 0 1 1/ 1 1 0 0/ 1 1 0 1/ 1 1 1 0/ 1 1 1 1/
4. (20 points) Implement a combinational logic circuit that negates a 4 bit number using 1's complement representation. IGNORE THE CARRY BIT. Each step is worth 5 points.
A) complete the given truth table
B) Fill out the k-maps (correct base 10 numbers help here)
C) loop the k-maps (get complete cover with a minimum number of loops)
D) write down the output functions in minimized sum of product form :