In this laboratory, we'll be using the Abel software package, an industry standard language for specifying programmable logic devices. One of the utilities provided by Abel is automated logic minimization. In this laboratory, we'll learn how to write Abel programs and how to use the Espresso logic minimization functions of Abel. The "Examples Folder" in the Abel folder also contains many example programs. You should consult the Abel manuals which Anand has for more details on how able works.
Espresso reduction uses a heuristic logic reduction algorithm to reduce combinational functions. Although it is not guaranteed to always produce optimally minimal expressions, it is close to optimal for small problems and is able to handle large functions that would be impossible to minimize manually.
The Abel Installation at UB
Abel's install requires that a temp directory be created in the in root of the DOS system. Also, You must check that the abel device library path name is set correctly in the autoexec.bat. The best method for checking this is to look at able on a working machine. If you still cannot get abel to work, see Zahid.
The Abel Programming Language
The first example we will use to demonstrate Abel is the increment/decrement function. We will first specify a combinational circuit for this function and then extend this to build a counter. On the following pages are Abel files that specify the increment/decrement function using three different methods: logic equations, truth table, and arithmetic operations. Please note that the numbers in the left margin have been added for explanatory purposes and should not be included in Abel files!
0) Comments
The preamble to this file is a comment section describing the pins of the Intel 5C032 PLD used by this program. When changing from one PLD to another, you typically must change the pin assignments to match the PLD pinout (see line 5.) All comments begin with a double quote and end with another, or a <RETURN> character, whichever comes first.
1) Module Statement
Modules are independent logic descriptions that are in the same file. The sample file given here consists of one module, but one file may contain multiple modules. Each module statement must be paired with a corresponding end statement (see line 9). The module name is used for the LogicWorks simulation model file and should not conflict with that used by other programs.
2) Options Statement (optional)
The Options statement gives command line options to Abel that indicate how the program is to be compiled. By default Abel assumes that all the options will be specified in the file. These can be overridden using the Options menu. In this case, we have chosen "bypin" optimization that will apply Espresso to each output separately. This is appropriate because we cannot share product terms in our device. We have also chosen the "fixed" option that will disable a Abel feature that finds the best implementation for an output by considering uncomplemented and complemented versions. We are requiring that the polarity be left as specified; however, there are cases where the complement of a function may fit when the uncomplemented version does not. The Abel manual gives a full list of options.
0. "Intel 5C032 PLD Pin Configuration " "Input/CLK: 1 " "Input/VPP: 11 " "Inputs: 2, 3, 4, 5, 6, 7, 8, 9 " "Input/Output: 12, 13, 14, 15, 16, 17, 18, 19 " 1. module UpDownTT 2. options '-reduce bypin fixed' "bypin -> optimize each output" separately "fixed -> do not alter output polarity " 3. title 'Up/Down counter Demo File' 4. UpDownTT device 'E0320'; 5. D1,D2,D3 pin 1,2,3; "Inputs" Q1,Q2,Q3 pin 12,13,14 istype 'com'; "Outputs" IncDec pin 4; "Increment/Decrement control" 6. Input = [D3,D2,D1]; "3-bit number" Output = [Q3,Q2,Q1]; "3-bit number" 7. truth_table ( [Input, IncDec] -> Output) [ 0, 1] -> 1; [ 1, 1] -> 2; [ 2, 1] -> 3; [ 3, 1] -> 4; [ 4, 1] -> 5; [ 5, 1] -> 6; [ 6, 1] -> 7; [ 7, 1] -> 0; [ 0, 0] -> 7; [ 1, 0] -> 0; [ 2, 0] -> 1; [ 3, 0] -> 2; [ 4, 0] -> 3; [ 5, 0] -> 4; [ 6, 0] -> 5; [ 7, 0] -> 6; 8. test_vectors ( [Input, IncDec] -> Output) [ 0, 1] -> 1; [ 1, 1] -> 2; [ 2, 1] -> 3; [ 3, 1] -> 4; [ 4, 1] -> 5; [ 5, 1] -> 6; [ 6, 1] -> 7; [ 7, 1] -> 0; [ 0, 0] -> 7; [ 1, 0] -> 0; [ 2, 0] -> 1; [ 3, 0] -> 2; [ 4, 0] -> 3; [ 5, 0] -> 4; [ 6, 0] -> 5; [ 7, 0] -> 6; 9. end UpDownTT UpDownTT.abl
3) Title Statement (optional)
The title statement allows you to incorporate a documentation string into a module. The title string is used for documentation purposes only and is included in Abel generated JEDEC files (used to actually program the devices) and documentation files.
4) Device Declaration
The device declaration indicates which PLD device is to be used, in this case the Intel 5CE032, which is compatible with the Altera E0320. The string "UpDownTT" is used to identify the device and for the name of the JEDEC output file; you may change it if you wish.
5) Pin Declarations
You need to associate the signals of your function with pins of the PLD. The comment block at the beginning of the program gives the pins of the PLD we are using. Obviously, input and output pins must be assigned consistent with the PLD. We also specify that our outputs are "combinational" using the "com" signal type.
6) Set Declarations
Set declarations are used to associate signals into groups. Signals in a set can be treated collectively as an n-bit number in the Abel program. For example, you could assign a two-signal set the values 0, 1, 2, or 3. In the example above, the inputs and outputs of the increment/decrement function are grouped to make the truth table declaration easier.
NOTE: Always use full set notation instead of integers; that is, 5 is represented as [0,1,0,1], except in the truth table and test vectors. Abel may appear to generate incorrect results otherwise because of the way it expands integers into their bit string representations. Binary numbers can also be represented by using the ^b prefix. The default is decimal but the ^b prefix can be used for binary numbers, and ^o for octal and ^h for hexadecimal numbers (e.g., ^b101, ^o77, ^h1f).
7) Truth Table
You can specify functions either as logic equations or as a truth table. In this program, the function is specified as a truth table. Note that this function is completely specified. That is, output values are given for all input combinations, meaning that there are no "don't cares."
8) Test Vectors
Abel allows you test the results of the program compilation via test vectors. Simulation is performed using the fuse map file produced by Abel and will find bugs in the compilation process as well as bugs in your program. This allows you to check the work of the program and, in general, make sure that you got what you wanted as a result. Note here that the test vectors look just like the truth table.
9) End Statement
The end statement marks the end of the module. If a name is given, it must match that in the module statement at the beginning of the file (see line 1).
Compiling a Abel Program
Compiling a Abel specification into reduced logic equations (and programming information for PLD's) takes 6 steps:
1) The input file is PARSEd. This will catch syntax errors.
2) The equations are TRANSFORMed into Boolean logic equations.
3) The Boolean equations are REDUCEd using the Espresso method we discussed in the lecture.
4) The standard FUSEMAP output file is produced. This file is used by the programmer to configure the PLD (where to make and not make connections in the AND/OR arrays).
5) The output equations are SIMULATEd using test vectors supplied by the user.
6) DOCUMENTation is produced. In particular, the .doc file is written with the reduced equations.
Abel is launched by either double-clicking the Abel icon or a Abel file. You can create an Abel program file directly in Abel by using the New command under the File menu to open an empty file window and using standard Macintosh editing commands. Alternatively, you can create your program with another application, such as Word or MacWrite, and save the file as a text-only document and open the file within MacAbel. The method of choice is to use an existing Abel program such as the demo files given here as a template or skeleton for your program. (Be careful not to type control characters into a Abel input file as they are invisible on the screen but will cause cryptic syntax error messages. You can see the control characters if you open the file using Word.)
Start up Abel on the demo file above. There is an Options menu that allows you to interactively specify how Abel processes your file. We will generally use the FLAG statement as shown above to do this, but it is sometime convenient to quickly change the settings using this menu. The manual describes the various options, but you should leave these alone until you know that you need them.
To compile the program, choose the Abel command under the Run menu. Abel will spend some time performing the six stages of execution. When the Run command is complete, several new documents will have been generated. (NOTE: only the first eight characters of the file name are used with the different file extensions so you must make sure that whatever file names you use differ in the first eight characters.) The document we're interested in for now has the name of your original Abel program file suffixed with `.doc'. You can view this document with a text editor such as Word or look at the compiled and optimized equations using the View menu in MacAbel. This latter method is preferred. You can also view the fusemap that was produced for the device and the results of applying the simulation vectors. Look at the optimized output equations. Are they what you expected?
Now take a look at the following program. This program specifies the same circuit-using equations instead of a truth table. Note the use of the WHEN-THEN-ELSE construct, which is similar to the IF-THEN-ELSE of other programming languages. Note, however, that the THEN and ELSE clauses can have only one statement, not a block of statements. (A not-too-serious deficiency--to obtain the same effect as a block of statements, you can use set notation, e.g. "[x,y,z] = [0,1,1]" .)
module UpDownEQ options '-reduce bypin fixed' "bypin -> optimize each output" separately "fixed -> do not alter output polarity " title 'Up/Down counter Demo File'
UpDownEQ device 'E0320'; D1,D2,D3 pin 1,2,3; "Inputs" Q1,Q2,Q3 pin 12,13,14 istype 'com'; "Outputs" IncDec pin 4; "Increment/Decrement control" Input = [D3,D2,D1]; "3-bit number" Output = [Q3,Q2,Q1]; "3-bit number" equations WHEN (IncDec) THEN Q3 = D3 $ (D2 & D1); " $ is XOR " ELSE " # is OR " Q3 = D3 $ (!D2 & !D1); " & is AND " WHEN (IncDec) THEN Q2 = D2 $ D1; ELSE Q2 = D2 $ !D1; Q1 = !D1; test_vectors ( [Input, IncDec] -> Output) [ 0, 1] -> 1; [ 1, 1] -> 2; [ 2, 1] -> 3; [ 3, 1] -> 4; [ 4, 1] -> 5; [ 5, 1] -> 6; [ 6, 1] -> 7; [ 7, 1] -> 0; [ 0, 0] -> 7; [ 1, 0] -> 0; [ 2, 0] -> 1; [ 3, 0] -> 2; [ 4, 0] -> 3; [ 5, 0] -> 4; [ 6, 0] -> 5; [ 7, 0] -> 6; end UpDownEQ UpDownEQ.abl
The next program uses arithmetic operators to define this function. These operators are automatically expanded by Abel into logic operators. The use of these operators can greatly simplify programs. Note also the use of the meta-programming language used to generate the truth table for the test vectors. These statements are part of a macro language that is executed before the program is compiled. In this case, these statements expand to the same truth table as above except that the increment and decrement test vectors are interleaved.
module UpDownAR
options '-reduce bypin fixed' "bypin -> optimize each output" separately
"fixed -> do not alter output polarity
" title 'Increment/Decrement Demo File'
UpDownAR device 'E0320';
D1,D2,D3 pin 1,2,3; "Inputs"
Q1,Q2,Q3 pin 12,13,14 istype 'com'; "Outputs"
IncDec pin 4; "Increment/Decrement control"
Input = [D3,D2,D1]; "3-bit number"
Output = [Q3,Q2,Q1]; "3-bit number"
equations
WHEN (IncDec == 1) THEN
Output = Input + [0,0,1]; "Do not use '+ 1'!
" ELSE Output = Input - [0,0,1];
@const n=8;
test_vectors ( [Input, IncDec] -> Output)
[ 0, 0] -> 7;
[ 0, 1] -> 1;
@const i=1; @repeat n-2 {
[ i, 0] -> @expr i-1;;
[ i, 1] -> @expr i+1;;
@const i=i+1;}
[ 7, 0] -> 6;
[ 7, 1] -> 0;
end UpDownAR
UpDownAR.abl
Up to now, we have used only one type of PAL. There are literally hundreds to choose from, and Abel knows about most of them. When specifying a different PAL, you must make sure you use the correct input and output pins. Changing from one PAL to another, or even a PROM, is generally just a simple matter of changing the pin declarations.
Minimization Experiments
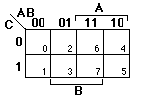
1. Let us begin with a simple three-variable function: F(A,B,C) = [[Sigma]]m(3,4,5,6,7). First, fill in the K-map below, and determine the reduced two-level sum-of-products expression by hand. Now, using the input format as described above, prepare an input file describing the function. Run Abel and examine the output truth table it produces. How does the result compare with your hand-determined result?

By hand: F =
Abel: F =
Repeat the process of finding the minimum sum-of-products form with the following three- and four-variable functions:
2. F(A,B,C) = [[Sigma]]m(0,4,6,7)
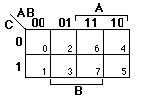
By hand: F =
Abel: F =
3. F(A,B,C,D) = [[Sigma]]m(0,2,3,5,6,7,8,10,11,14,15)
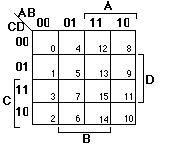
By hand: F =
Abel: F =
Multiple-Output Function Minimization
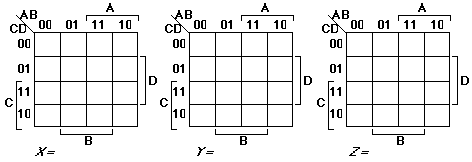
The examples we've worked with so far have involved a single output function. Now enter the truth table for the two-bit binary adder described by the truth table below. Minimize the K-maps on your own in the maps provided on the next page. Write down the Boolean equations for your reduced solution.
4. Repeat the process using Abel, using the "group" option instead of "bypin" to optimize the outputs together rather than separately. How does Abel's solution compare with your own? If they are not exactly the same, it may not be because you made a mistake, but rather that Abel found an alternative cover. If they are different, is the complexity of the covers the same, that is, do both solutions use the same number of product terms and literals?
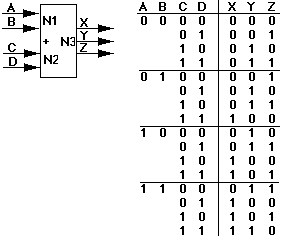
Creating LogicWorks PLD Devices
There are two ways we can use simulation to double-check a Abel program before actually programming, and possibly wasting, a PLD. First, Abel has a built-in simulator to which you can provide a set of test vectors as shown in the examples. Second, we can instantiate a PAL or PROM based on the Abel output and include it in a LogicWorks simulation. In this section, you will learn how to include PLDs described in Abel in your LogicWorks circuits.
First you must make the file that is used by LogicWorks to create a PLD device to be used in the simulation. Invoke the Simulate Options... command in the Abel Options menu. Look for an entry that indicates that a DesignWorks file is to be created (look in the lower left-hand corner). This .dwl file is in a format that LogicWorks can use to create the simulation device corresponding to the PLD specified using MacAbel. Compile your program again with this switch turned on. Now we will use LogicWorks to create a simulation to test the counter.
After entering LogicWorks, invoke the FromAbel module in the Modules menu. This will ask you for the DesignWorks format .dwl file you just created. LogicWorks will now create a device based on this file, complete with signal names and internal functionality, and allow you to save it in a new library (give it a name that starts with your initials). Once the device is in the library, you can instantiate the device by selecting it as you would any other device in the Libraries menu. Remember to use your own personal library for hierarchical and PLD devices you create.
5. Take one of the Abel programs above for the increment/decrement function and compile it into a PAL device in LogicWorks. Verify your device and demonstrate it to the professor.
6. Use MacABEL to design a 3-bit comparator with two inputs A and B and one output signal GT, which is 1 if A > B. Compile this into a PLD device in LogicWorks and verify the result. Demonstrate your circuit to the professor.
7. Write a Abel program for computing the "game of life" function using the 5C032 PLD. Note that each output of the PLD has a PLA block with eight product terms. If your circuit has more than eight terms for its single output you will need to partition the logic across multiple PLA blocks by creating intermediate signals (outputs that are fed back as inputs).
LogicWorks Laboratory Three
Introduction to Abel for Combinational Logic
Summary Sheet
(Include this as the cover for what you hand in.)
Name:__________________________________________________________________
1. Demonstrate the increment/decrement PLD device in
LogicWorks.
Prof's Initials:
2. Demonstrate the 3-bit comparator PLD device in LogicWorks.
Prof's Initials:
3. Demonstrate the Game of Life PLD device in LogicWorks.
Prof's Initials: