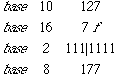
Digital Design I
Course Number: CR245
Outline
you will be responsible for Appendix A, Number systems as well as chapters 1-9 in addition to any chapters covered in class. Topics include, but are not limited to, the following:
Combinatorial Logic:
1 Introduction to number systems
2-3 Boolean Algebra
5 Applications of Boolean Algebra
6 K-maps
8 Multi-level Gate Networks, Nand and NOR gates
9 Multiple-output networks, Mux's,
Decoders, ROMs and PLA's
Sequential Logic:
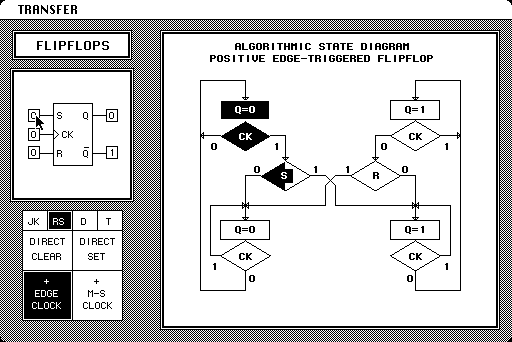
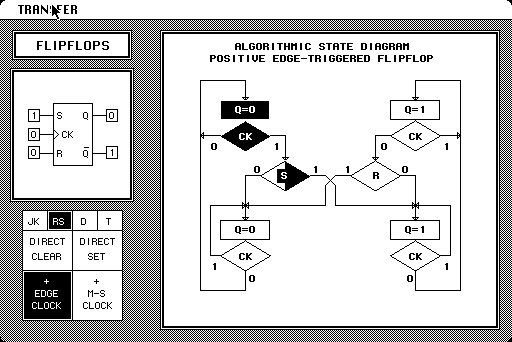
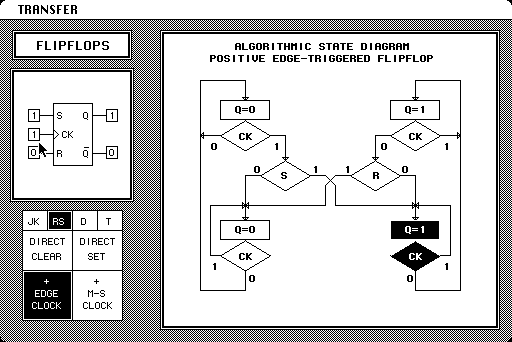
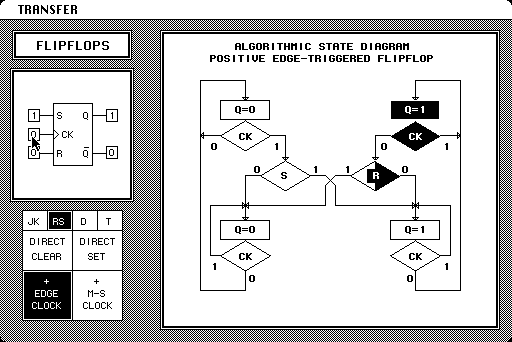
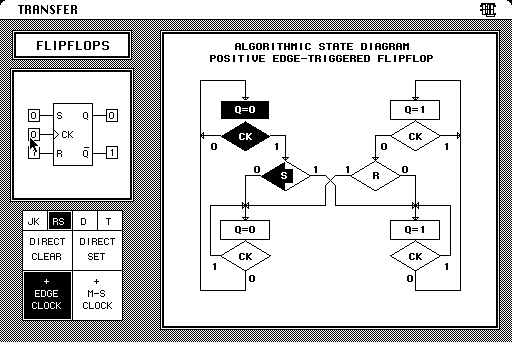
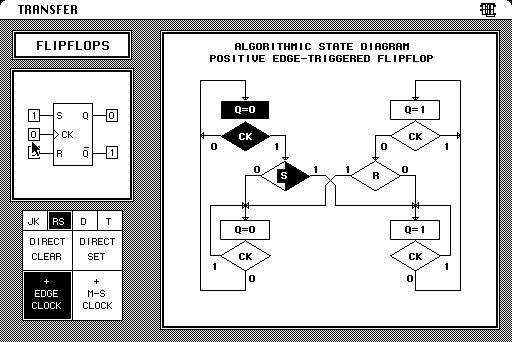
11 Flip-flops
12 Counters and Sequential Nets
13 Analysis of Clocked Sequential Nets
14 Derivation of State Graphs and Tables
15 Reduction of State tables State Assignment
18 MSI IC's in Sequential Nets
20 Nets for + and -
21 Nets for * and /
22 State Machines and SM Charts
Introduction to Number Systems and Conversions
System => a collection of interacting units.
State variable => provides minimum amount of information which, together with the system model and input determines the state at any later time.
Analog System => state variables have real number values
Digital System => state variables have integer values
Combinatorial network => state is a function of input
Sequential net => combinatorial net + memory and so depends on history.
Number systems and conversion
R=radix
for example
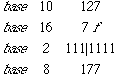
decimal integer, N, to base R using the division method:
![]()
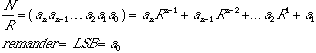
2.3 Boolean Expressions
Literal = each appearance of a variable or it's complement.
abcd + qrstu = 9 literals
dd'abd'= 5 literals
The number of literals = the number of gate inputs
truth tables list all combinations via perfect enumeration.
Basic Theorems
operations with zero and one
x+0=x
x+1=1
i.e.(ab'+d)+1=1
x*1=x
x*0=0
Idempotent Laws
x+x=x
x*x=x
Involution Law
(x')'=x
x*x'=0
i.e. (ab'+d)(ab'+d)'=0
Laws of Complementary
x+x'=1
x*x'=0
i.e. (ab'+d)(ab'+d)'=0
2nd dist. law
x+yz=(x+y)(x+z)
Proof:
(x+y)(x+z)=xx+xz+yx+yz
by x*x=x (2-6d)
=x+xz+yx+yz factor out x
=x(1+z+y)+yz
by (2-5) x+1=1
=x+yz
Q.E.D
Proof by perfect enumeration
x y z 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1